Закон Мура с позиций математики
С позиций математики закон Мура представляется простым выражением:

где N0 – количество транзисторов на кристалле N в некоторый год y (условно считаем его нулевым), N(y) – число транзисторов на кристалле спустя y лет и yy – срок (в годах и долях года), за который число транзисторов возрастает вдвое.
Насколько данные таблицы соответствуют представленной формуле? И возможен ли по ним прогноз? Попробуем ответить по возможности строго на эти вопросы. Для этого, используя программу компьютерной математики Mathcad, нанесем на график в логарифмическом масштабе точки, соответствующие приведенным в таблице данным. Подберем отрезки прямых, которые максимально близко проходят через эти точки (рис. 2.7).
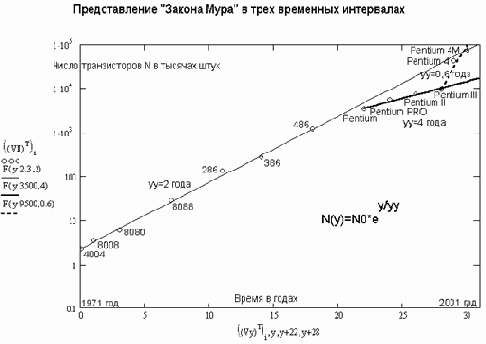
Рис. 2.7. Графическое представление закона Мура в системе Mathcad
Обработка представленных данных дает поразительные результаты. Оказывается, целых 22 года число транзисторов и впрямь увеличивалось вдвое за каждые yy=2 года. При этом исходные точки укладываются почти точно на представляющую их приближенную зависимость.
Однако с появлением процессоров класса Pentium действие даже скорректированного закона Мура стало грубо нарушаться. Попробуем подобрать прямую для хорошего представления реалий роста числа транзисторов после этого периода, задав в качестве отсчета момент появления процессоров Pentium – точку (22, 1200). Оказывается (жирная прямая на рис. 3), время удвоения возросло почти вдвое и составило yy=4 года. Это стало свидетельством предкризисной ситуации в развитии технологии микропроцессоров.
Но затем, при переходе от производства процессора Pentium III к Pentium 4 в 1999 году, кривая роста числа транзисторов во времени резко скакнула вверх начиная с точки (28, 9500). Это, очевидно, связано с вводом новых технологических решений и переходом на технологию 0,13 мкм. Время удвоения при этом уменьшилось до рекордно малой величины в 0,6 года, но его оценка пока математически весьма недостоверна из-за малого объема выборки данных после 1999 года – всего 3 точки.